DIFFRACTION IN OPTICS
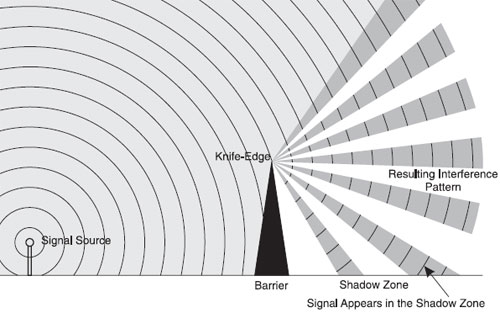
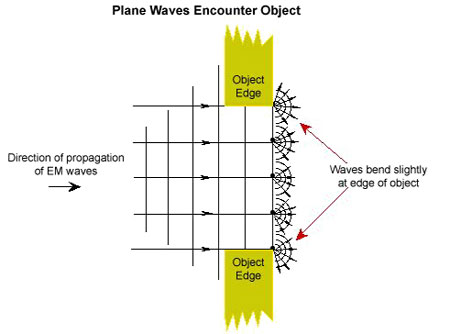
Diffraction refers to various phenomena which occur when a wave encounters an obstacle or a slit. In classical physics, the diffraction phenomenon is described as the interference of waves according to the Huygens–Fresnel principle. These characteristic behaviors are exhibited when a wave encounters an obstacle or a slit that is comparable in size to its wavelength. Similar effects occur when a light wave travels through a medium with a varying refractive index, or when a sound wave travels through a medium with varying acoustic impedance. Diffraction occurs with all waves, including sound waves, water waves, and electromagnetic waves such as visible light, X-raysand radio waves.

The effects of diffraction are often seen in everyday life. The most striking examples of diffraction are those that involve light; for example, the closely spaced tracks on a CD or DVD act as a diffraction grating to form the familiar rainbow pattern seen when looking at a disk. This principle can be extended to engineer a grating with a structure such that it will produce any diffraction pattern desired; the hologram on a credit card is an example. Diffraction in the atmosphere by small particles can cause a bright ring to be visible around a bright light source like the sun or the moon. A shadow of a solid object, using light from a compact source, shows small fringes near its edges. The speckle pattern which is observed when laser light falls on an optically rough surface is also a diffraction phenomenon. When deli meat appears to be iridescent, that is diffraction off the meat fibers.[3] All these effects are a consequence of the fact that light propagates as a wave.

Interference and Diffraction
The terms "interference" and "diffraction" were originally used with the Newtonian corpuscular theory of light, but were taken over to describe the same phenomena in the new wave theory. What is called "interference" refers to the operation of the principle of superposition: the amplitudes in two light fields simply add, but in no way affect each other or "interfere". This is a fundamental property of the Huygens-Fresnel theory of the propagation of light, and appears in every application of it. However, it may be useful to think of "interference" in a restricted sense as involving a countable number of beams (often two) with the characteristic appearance offringes, periodic spatial variations in intensity.
"Diffraction" may refer to all the phenomena observed near shadows, or may be limited to the property of waves to bend around an obstacle. If used in this restricted sense, then the observed fringes are a result of interference of the diffracted waves with others. The apparent absence of diffraction of light was strong evidence against a wave theory. However, diffraction of light was eventually recognized (by Grimaldi, 1665) at a remarkably late date. It was also a prediction of Huygens' wavelet theory, invented to explain double refraction. However, there was no periodicity in Huygens' theory, and no explanation of fringes.
Fresnel combined the periodicity of light discovered by Young with the wavelet idea of Huygens. Each point on a wavefront at a given instant is the source of a spherical wavelet. The sum of the wavelets emitted from all points on the wavefront at an observation point P is the resultant amplitude there, and the intensity is the square of this amplitude. This Huygens-Fresnel principle, published in 1818, is remarkably in accord with observations.
There are several reasons why diffraction phenomena are so difficult to observe that they were not recognized until Grimaldi's time. These are: lack of coherence in the light source; insufficient intensity of the light source; and small size of the pattern. Coherence is the ability to produce interference fringes, demanding stable phase relations both in time and space, called temporal and spatial coherence, respectively. White light, with wavelengths between 400 and 700 nm, can produce fringes only in low orders, as in oil films or Newton's rings. Good temporal coherence demands monochromaticity. The coherence time is roughly the reciprocal of the frequency bandwidth. Spatial coherence means that the fringes will fall at definite locations, not smeared out over the observing screen, as happens with broad sources. They may indeed produce fringes, but they overlap and cannot be seen. The Sun is a bright source of nearly parallel light, but not parallel enough to make diffraction fringes distinct.
Coherence can be provided by using a spectral lamp (sodium, or mercury with a filter) and a pinhole, perhaps preceded by a condensing lens. The disadvantage, however, is a greatly reduced intensity. If the fringes to be viewed are linear, the intensity can be greatly increased by using a slit, oriented parallel to the fringes. At the present time, a laser gives bright coherent light that will exhibit fringes around any shadow. The beam has to be expanded by using a short-focus lens.

Interference and diffraction are the main phenomena which demonstrate the wave nature of the light. There are many optical devices, where these phenomena can be observed. Diffraction grating is one of them, which allows a beam of light to be resolved into different colors. Diffraction grating consists usually of thousands of narrow, closely spaced parallel slits (or grooves). The use of diffraction gratings DG10 and laser pointer allows these effects to be easily demonstrated and investigated at home, school, university, etc. At this website we consider the basic theory of Fraunhofer diffraction at one, double and multiple slit as well as the real experiments with diffraction gratings DG10, Fresnel zone plates FZP-01 and Gabor hologram HH-4000.




You can order diffraction gratings DG10, Fresnel zone plates FZP-01 and Gabor hologram HH-4000 with KAGI online payment processing system and use them for educational and scientific purposes. We shall send the ordered items to you by mail after the payment confirmation.
Huygens' Principle
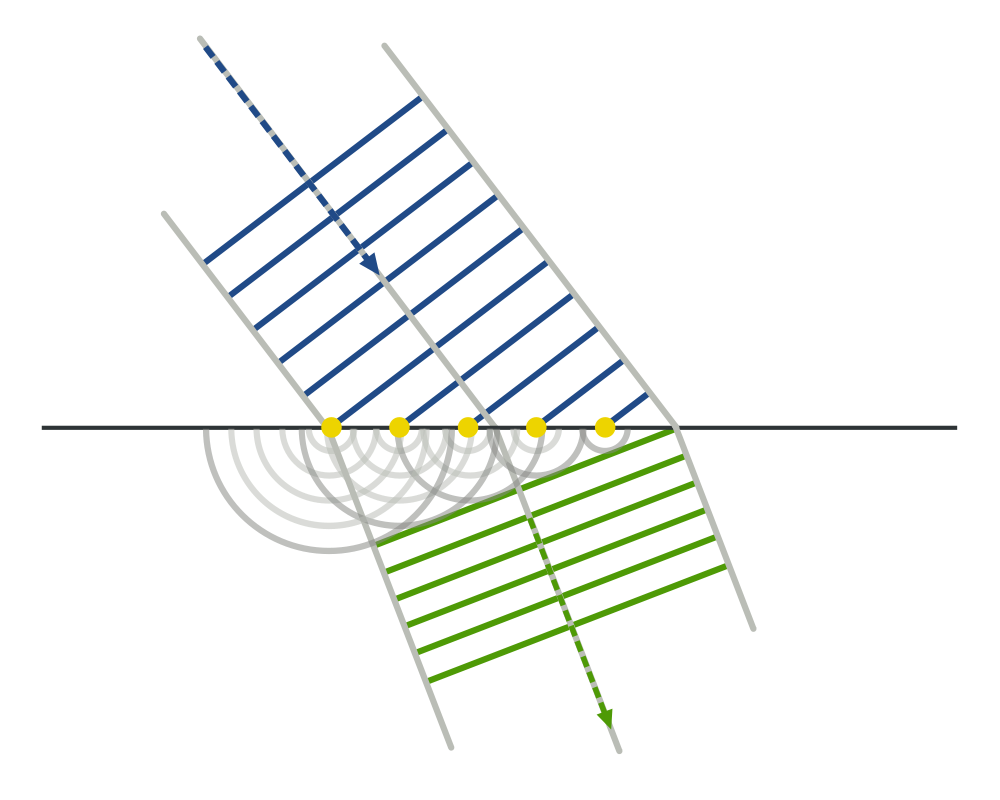
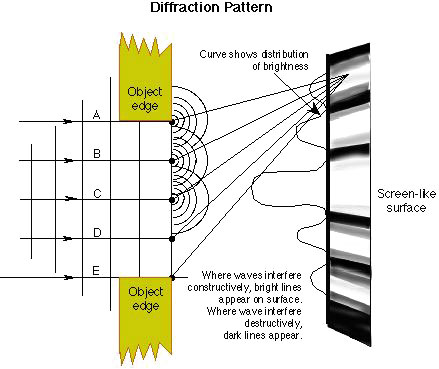
Christian Huygens, a contemporary of Newton's, thought light was a wave and proposed a theory or principle that is still useful in understanding the propagation of waves.Huygens' Principle is that every point on a wavefront is the source of new wavelets and the new wavefront is the envelope of these wavelets.
As a wave encounters an obstruction &emdash; like a slit edge &emdash; the new wave bends around this obstruction.
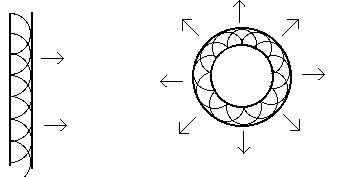
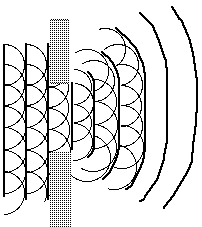
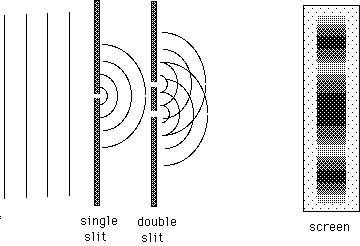
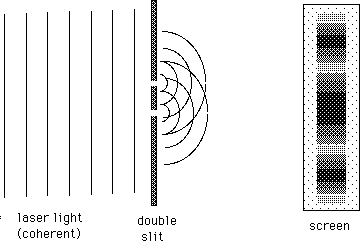
Young's Double Slit
In 1801, British Physicist Thomas Young conducted an experiment that gave conclusive experimental evidence to the wave nature of light.
He passed coherent light through two slits and observed a series of bright and dark fringes that can only be explained by the constructive and destructive intereference of waves.


Diffraction Grating
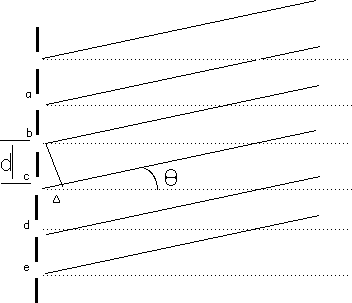

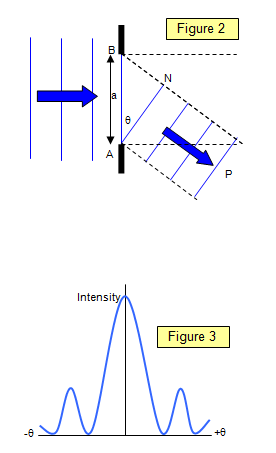
The big distinction, with a diffraction grating, is how rapidly the intensity falls away from these maxima. Because there are so many slits to act as sources, any angle other than those for maxima will be dark or nearly dark.
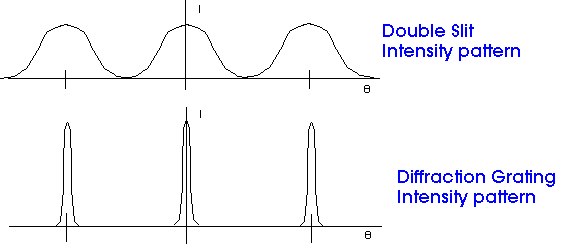
Diffraction
We typically use the word "interference" to describe the superposition and interaction of a few waves as in Young's Double Slit Experiment.
We typically use the word "diffraction" to describe the superposition and interaction of many waves as in the Diffraction Grating or the diffraction effects of a single slit or the diffraction effects of a circular opening or the diffraction effects of light as it goes around any object.
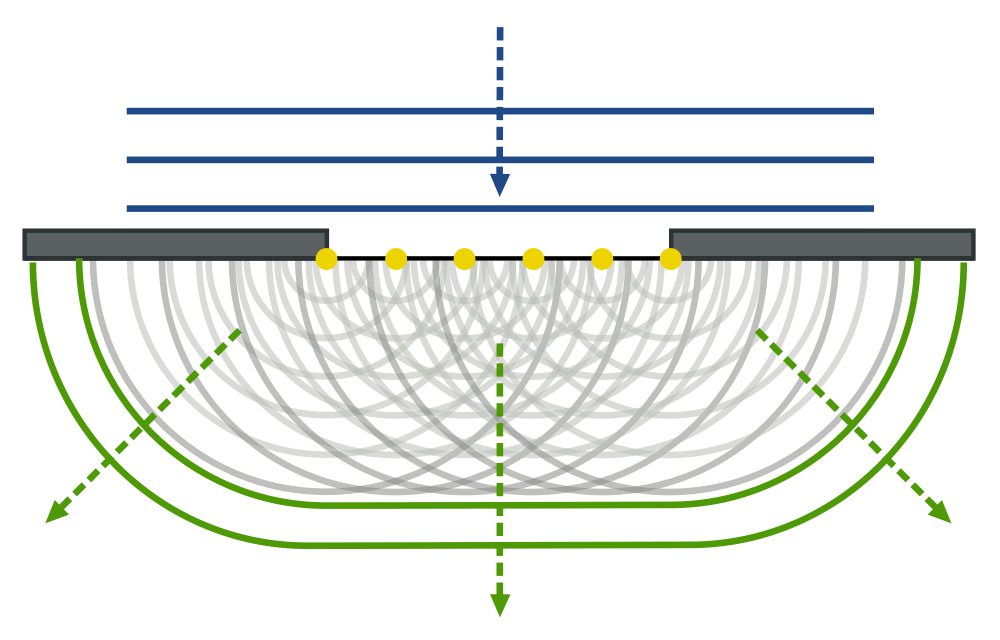
We will look at the diffraction of a single slit.

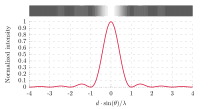
In the straight forward direction, light from all parts of the slit travels the same distance and arrives "in phase" so there is a bright central maximum.



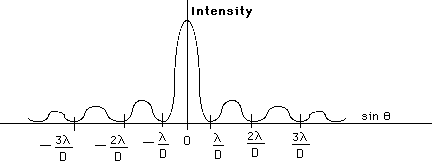
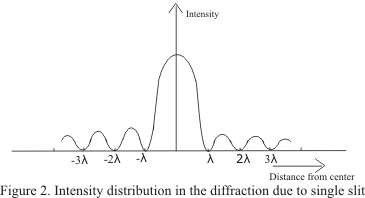
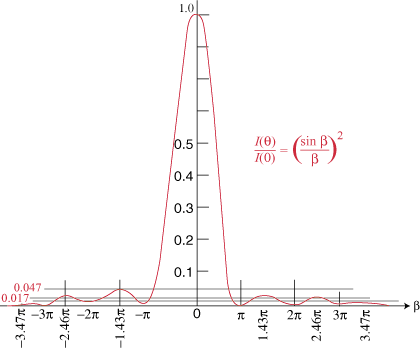
A single slit diffraction pattern has a bright central maximum surrounded by much smaller maxima.
Optical Resolution
If we look closely enough, every image is surrounded by a diffraction pattern produced by the wave nature of light as it passes through an opening like the edge of a lens.
The diffraction pattern produced by a circular opening is very similar to that produced by a single slit.
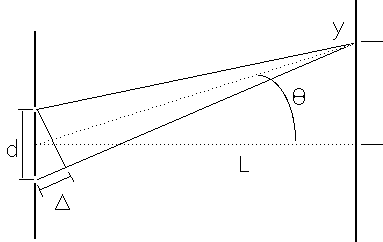
For a slit, the angular distance from the center of the central maximum to the first minimum is
For a circular opening, the angular distance from the center of the central maximum to the first minimum is
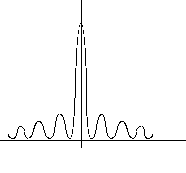
If we look at two stars that have a large angular separation, their diffraction patterns hardly overlap, and we clearly distinguish that there are two stars.
The same would be true of two items of cell structure when viewed through a microscope.
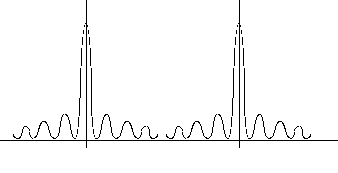
As the two objects come closer, their diffraction patterns overlap and it may become difficult to distinguish the two images.
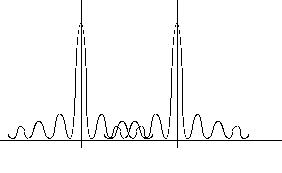
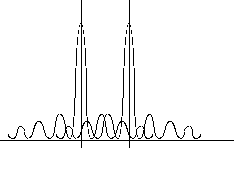
"Rayleigh's criterion" for the resolution of two point sources is that the first minimum of one diffraction pattern occurs at the central maximum of the other one.
Untrained eyes will loose distinction before this and well trained eyes may distinguish two sources even closer than Rayleigh's criterion.
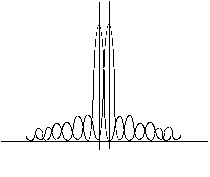
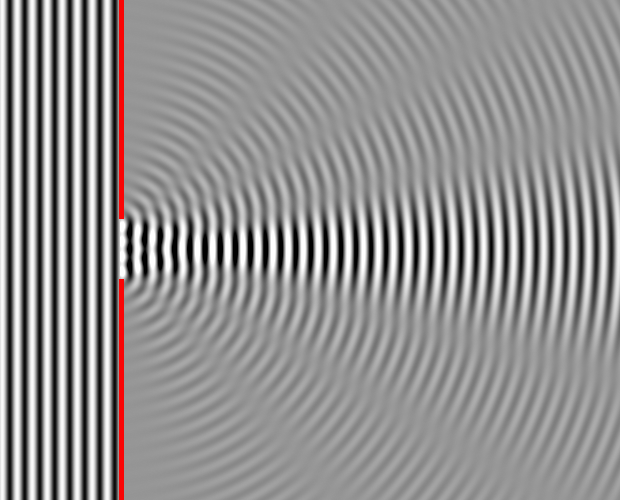
This is an attempt to more clearly visualize the nature of single slit diffraction. The phenomenon of diffraction involves the spreading out of waves past openings which are on the order of the wavelength of the wave. The spreading of the waves into the area of the geometrical shadow can be modeled by considering small elements of the wavefront in the slit and treating them like point sources.
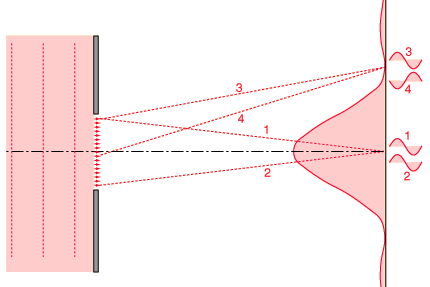
If light from symmetric elements near each edge of the slit travels to the centerline of the slit, as indicated by rays 1 and 2 above, their light arrives in phase and experiences constructive interference. Light from other element pairs symmetric to the centerline also arrive in phase. Although there is a progressive change in phase as you choose element pairs closer to the centerline, this center position is nevertheless the most favorable location for constructive interference of light from the entire slit and has the highest light intensity.
The first minimum in intensity for the light through a single slit can be visualized in terms of rays 3 and 4. An element at one edge of the slit and one just past the centerline are chosen, and the condition for minimum light intensity is that light from these two elements arrive 180° out of phase, or a half wavelength different in pathlength. If those two elements suffer destructive interference, then choosing additional pairs of identical spacing which progress downward across the slit will give destructive interference for all those pairs and therefore an overall minimum in light intensity.
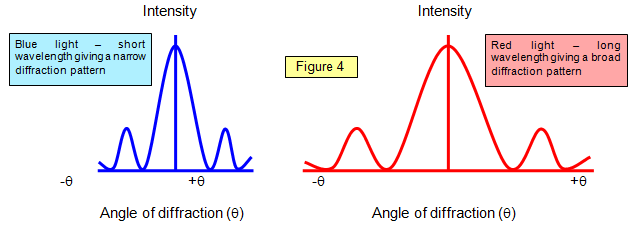
One of the characteristics of single slit diffraction is that a narrower slit will give a wider diffraction pattern as illustrated below, which seems somewhat counter-intuitive. One way to visualize it is to consider that rays 3 and 4 must reach one half wavelength difference in light pathlength, and if the slit is narrower, it will take a greater angle of the rays to achieve that difference.
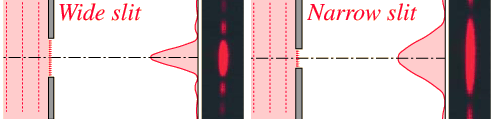
The first minimum in intensity for the light through a single slit can be visualized in terms of rays 3 and 4. An element at one edge of the slit and one just past the centerline are chosen, and the condition for minimum light intensity is that light from these two elements arrive 180° out of phase, or a half wavelength different in pathlength. If those two elements suffer destructive interference, then choosing additional pairs of identical spacing which progress downward across the slit will give destructive interference for all those pairs and therefore an overall minimum in light intensity.
One of the characteristics of single slit diffraction is that a narrower slit will give a wider diffraction pattern as illustrated below, which seems somewhat counter-intuitive. One way to visualize it is to consider that rays 3 and 4 must reach one half wavelength difference in light pathlength, and if the slit is narrower, it will take a greater angle of the rays to achieve that difference.

he diffraction patterns were taken with a helium-neon laser and a narrow single slit. The slit widths used were on the order of 100 micrometers, so their widths were 100 times the laser wavelength or more. A slit width equal to the wavelength of the laser light would spread the first minimum out to 90° so that no minima would be observed. The relationships between slit width and the minima and maxima of diffraction can be explored in thesingle slit calculation.
|
 | (1) | ||
 | (2) |
where C is a constant, k is the wave number, and
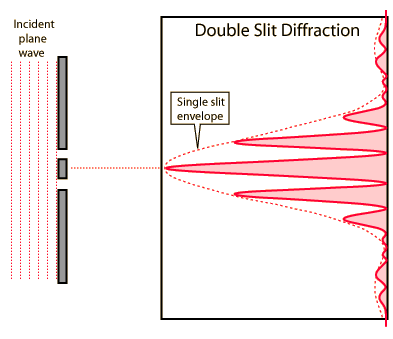
The pattern formed by the interference and diffraction of coherent light is distinctly different for a single and double slit. The single slit intensity envelope is shown by the dashed line and that of the double slit for a particular wavelength and slit width is shown by the solid line. The photographs of the single and double slit patterns produced by a helium-neon laser show the qualitative differences between the patterns produced. You can see that the drawing is not to the same scale as the photographs, but the breaking up of the broad maxima of the single slit pattern into more closely spaced maxima is evident. The number of bright maxima within the central maximum of the single-slit pattern is influenced by the width of the slit and the separation of the double slits.

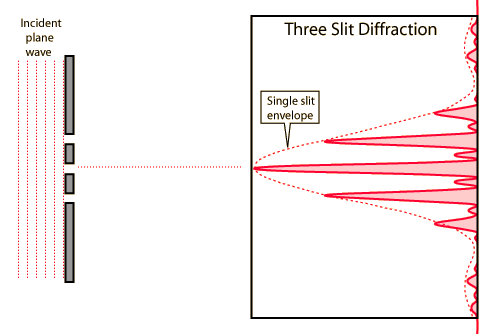
Three Slit Diffraction
Five Slit Diffraction
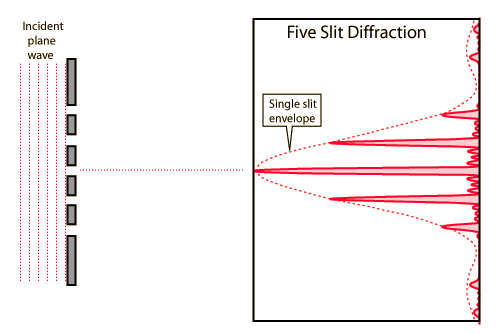
Under the Fraunhofer conditions, the light curve (intensity vs position) is obtained by multiplying the multiple slit interference expression times the single slit diffraction expression. The multiple slit arrangement is presumed to be constructed from a number of identical slits, each of which provides light distributed according to the single slit diffraction expression. The multiple slit interference typically involves smaller spatial dimensions, and therefore produces light and dark bands superimposed upon the single slit diffraction pattern.


The pattern formed by the interference and diffraction of coherent light is distinctly different for a single and double slit. The single slit intensity envelope is shown by the dashed line and that of the double slit for a particular wavelength and slit width is shown by the solid line. The photographs of the single and double slit patterns produced by a helium-neon laser show the qualitative differences between the patterns produced. You can see that the drawing is not to the same scale as the photographs, but the breaking up of the broad maxima of the single slit pattern into more closely spaced maxima is evident. The number of bright maxima within the central maximum of the single-slit pattern is influenced by the width of the slit and the separation of the double slits.



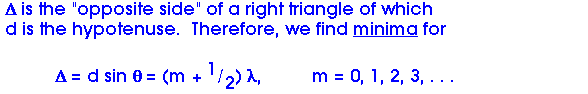


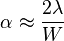



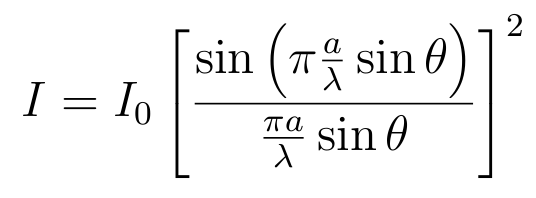


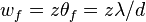




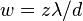

No comments:
Post a Comment