QUARTER AND HALF WAVE PLATES
Waveplate
A waveplate or retarder is an optical device that alters the polarization state of a light wave travelling through it. Two common types of waveplates are the half-wave plate, which shifts the polarization direction of linearly polarized light, and thequarter-wave plate, which converts linearly polarized light into circularly polarized light and vice versa.[1] A quarter wave plate can be used to produce elliptical polarization as well.


Principles of operation
A waveplate works by shifting the phase between two perpendicular polarization components of the light wave. A typical waveplate is simply a birefringent crystal with a carefully chosen orientation and thickness. The crystal is cut into a plate, with the orientation of the cut chosen so that the optic axis of the crystal is parallel to the surfaces of the plate. This results in two axes in the plane of the cut: the ordinary axis, with index of refraction no, and the extraordinary axis, with index of refraction ne. The ordinary axis is perpendicular to the optic axis. The extraordinary axis is parallel to the optic axis. For a light wave normally incident upon the plate, polarization component along the ordinary axis travels through the crystal with a speed vo = c/no, while the polarization component along the extraordinary axis travels with a speed ve = c/ne. This leads to a phase difference between the two components as they exit the crystal. When ne < no, as in calcite, the extraordinary axis is called the fast axis and the ordinary axis is called the slow axis. For ne > no the situation is reversed.
Depending on the thickness of the crystal, light with polarization components along both axes will emerge in a different polarization state. The waveplate is characterized by the amount of relative phase, Γ, that it imparts on the two components, which is related to the birefringence Δn and the thickness L of the crystal by the formula
where λ0 is the vacuum wavelength of the light.
Half-wave plate

For a half-wave plate, the relationship between L, Δn, and λ0 is chosen so that the phase shift between polarization components is Γ = π. Now suppose a linearly polarized wave with polarization vector  is incident on the crystal. Let θ denote the angle between
is incident on the crystal. Let θ denote the angle between  and
and 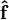 , where
, where 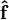 is the vector along the waveplate's fast axis. Let z denote the propagation axis of the wave. The electric field of the incident wave is
is the vector along the waveplate's fast axis. Let z denote the propagation axis of the wave. The electric field of the incident wave is
 is incident on the crystal. Let θ denote the angle between
is incident on the crystal. Let θ denote the angle between  and
and 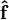 , where
, where 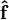 is the vector along the waveplate's fast axis. Let z denote the propagation axis of the wave. The electric field of the incident wave is
is the vector along the waveplate's fast axis. Let z denote the propagation axis of the wave. The electric field of the incident wave is
where 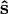 lies along the waveplate's slow axis. The effect of the half-wave plate is to introduce a phase shift term eiΓ = eiπ = −1 between thef and s components of the wave, so that upon exiting the crystal the wave is now given by
lies along the waveplate's slow axis. The effect of the half-wave plate is to introduce a phase shift term eiΓ = eiπ = −1 between thef and s components of the wave, so that upon exiting the crystal the wave is now given by
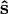 lies along the waveplate's slow axis. The effect of the half-wave plate is to introduce a phase shift term eiΓ = eiπ = −1 between thef and s components of the wave, so that upon exiting the crystal the wave is now given by
lies along the waveplate's slow axis. The effect of the half-wave plate is to introduce a phase shift term eiΓ = eiπ = −1 between thef and s components of the wave, so that upon exiting the crystal the wave is now given by
If  denotes the polarization vector of the wave exiting the waveplate, then this expression shows that the angle between
denotes the polarization vector of the wave exiting the waveplate, then this expression shows that the angle between  and
and 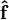 is −θ. Evidently, the effect of the half-wave plate is to mirror the wave's polarization vector through the plane formed by the vectors
is −θ. Evidently, the effect of the half-wave plate is to mirror the wave's polarization vector through the plane formed by the vectors 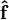 and
and  . For linearly polarized light, this is equivalent to saying that the effect of the half-wave plate is to rotate the polarization vector through an angle 2θ; however, for elliptically polarized light the half-wave plate also has the effect of inverting the light's handedness.[1]
. For linearly polarized light, this is equivalent to saying that the effect of the half-wave plate is to rotate the polarization vector through an angle 2θ; however, for elliptically polarized light the half-wave plate also has the effect of inverting the light's handedness.[1]
 denotes the polarization vector of the wave exiting the waveplate, then this expression shows that the angle between
denotes the polarization vector of the wave exiting the waveplate, then this expression shows that the angle between  and
and 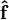 is −θ. Evidently, the effect of the half-wave plate is to mirror the wave's polarization vector through the plane formed by the vectors
is −θ. Evidently, the effect of the half-wave plate is to mirror the wave's polarization vector through the plane formed by the vectors 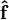 and
and  . For linearly polarized light, this is equivalent to saying that the effect of the half-wave plate is to rotate the polarization vector through an angle 2θ; however, for elliptically polarized light the half-wave plate also has the effect of inverting the light's handedness.[1]
. For linearly polarized light, this is equivalent to saying that the effect of the half-wave plate is to rotate the polarization vector through an angle 2θ; however, for elliptically polarized light the half-wave plate also has the effect of inverting the light's handedness.[1]
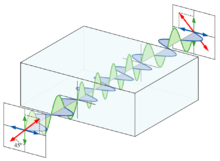
The half wave plate can be used to rotate the polarization state of a plane polarized light as shown in Figure 1.
 Suppose a plane-polarized wave is normally incident on a wave plate, and the plane of polarization is at an angle q with respect to the fast axis, as shown. After passing through the plate, the original plane wave has been rotated through an angle 2q.
Suppose a plane-polarized wave is normally incident on a wave plate, and the plane of polarization is at an angle q with respect to the fast axis, as shown. After passing through the plate, the original plane wave has been rotated through an angle 2q.
A half-wave plate is very handy in rotating the plane of polarization from a polarized laser to any other desired plane (especially if the laser is too large to rotate). Most large ion lasers are vertically polarized. To obtain horizontal polarization, simply place a half-wave plate in the beam with its fast (or slow) axis 45° to the vertical. The l/2 plates can also change left circularly polarized light into right circularly polarized light or vice versa. The thickness of half waveplate is such that the phase difference is 1/2 wavelength (l/2, Zero order) or certain multiple of 1/2-wavelength [(2n+1)l/2, multiple order].
Quarter-wave plate




For a quarter-wave plate, the relationship between L, Δn, and λ0 is chosen so that the phase shift between polarization components is Γ = π/2. Now suppose a linearly polarized wave is incident on the crystal. This wave can be written as
where the f and s axes are the quarter-wave plate's fast and slow axes, respectively, the wave propagates along the z axis, and Ef and Esare real. The effect of the quarter-wave plate is to introduce a phase shift term eiΓ =eiπ/2 = i between the f and s components of the wave, so that upon exiting the crystal the wave is now given by
The wave is now elliptically polarized.
If the axis of polarization of the incident wave is chosen so that it makes a 45° with the fast and slow axes of the waveplate, then Ef = Es ≡E, and the resulting wave upon exiting the waveplate is
and the wave is circularly polarized.
Quarter wave plate are used to turn plane-polarized light into circularly  polarized light and vice versa. To do this, we must orient the wave plate so that equal amounts of fast and slow waves are excited. We may do this by orienting an incident plane-polarized wave at 45° to the fast (or slow) axis, as shown in Figure 2. When a l/4 plate is double passed, i.e., by mirror reflection, it acts as a l/2 plate and rotates the plane of polarization to a certain angle, i.e., 90°. This scheme is widely used in isolators, Q-switches, etc.
polarized light and vice versa. To do this, we must orient the wave plate so that equal amounts of fast and slow waves are excited. We may do this by orienting an incident plane-polarized wave at 45° to the fast (or slow) axis, as shown in Figure 2. When a l/4 plate is double passed, i.e., by mirror reflection, it acts as a l/2 plate and rotates the plane of polarization to a certain angle, i.e., 90°. This scheme is widely used in isolators, Q-switches, etc.
 polarized light and vice versa. To do this, we must orient the wave plate so that equal amounts of fast and slow waves are excited. We may do this by orienting an incident plane-polarized wave at 45° to the fast (or slow) axis, as shown in Figure 2. When a l/4 plate is double passed, i.e., by mirror reflection, it acts as a l/2 plate and rotates the plane of polarization to a certain angle, i.e., 90°. This scheme is widely used in isolators, Q-switches, etc.
polarized light and vice versa. To do this, we must orient the wave plate so that equal amounts of fast and slow waves are excited. We may do this by orienting an incident plane-polarized wave at 45° to the fast (or slow) axis, as shown in Figure 2. When a l/4 plate is double passed, i.e., by mirror reflection, it acts as a l/2 plate and rotates the plane of polarization to a certain angle, i.e., 90°. This scheme is widely used in isolators, Q-switches, etc.
The thickness of the quarter waveplate is such that the phase difference is 1/4 wavelength (l/4, Zero order) or certain multiple of 1/4-wavelength [(2n+1)l/4, multiple order].
Quarter-Wave Plate Applications


The most common types of waveplates are quarter-wave plates (λ/4 plates) and half-wave plates (λ/2 plates), where the difference of phase delays between the two linear polarization directions is π/2 or π, respectively, corresponding to propagation phase shifts over a distance of λ / 4 or λ / 2, respectively.
Wave retarders are birefringent materials that alter (retard) the polarization state or phase of light traveling through them. A wave retarder has a fast (extraordinary) and slow (ordinary) axis.
As polarized light passes through a wave retarder, the light passing through the fast axis travels more quickly through the wave retarder than through the slow axis. In the case of a quarter wave retarder, the wave plate retards the velocity of one of the polarization components (x or y) one quarter of a wave out of phase from the other polarization component.
Polarized light passing through a quarter wave retarder thus becomes circularly polarized (see Figure 1). The action of the quarter wave is sometimes referred to as twisting or rotating the polarized light. Note that depending on which polarization component is retarded, one will have either a left handed or right handed circular polarizer.
Some important cases are:
- When a light beam is linearly polarized, and the polarization direction is along one of the axes of the waveplate, the polarization remains unchanged.
- When the incident polarization does not coincide with one of the axes, and the plate is a half-wave plate, then the polarization stays linear, but the polarization direction is rotated. For example, for an angle of 45° to the axes, the polarization direction is rotated by 90°.
- When the incident polarization is at an angle of 45° to the axes, a quarter-wave plate generates a state of circular polarization. (Other input polarizations lead to elliptical polarization states.) Conversely, circularly polarized light is converted into linearly polarized light.
Within a laser resonator, two quarter-wave plates around the gain medium are sometimes used for obtaining single-frequency operation(→ twisted-mode technique). Inserting a half-wave plate between a laser crystal and a resonator end mirror can help to reduce depolarization loss. The combination of a half-wave plate and a polarizer allows one to realize an output coupler with adjustable transmission.
Many waveplates are made of crystalline quartz (SiO2), as this material exhibits a wide wavelength range with very high transparency, and can be prepared with high optical quality. Other possible materials (to be used e.g. in other wavelength regions) are calcite (CaCO3), magnesium fluoride (MgF2), sapphire (Al2O3), mica (a silicate material), and some birefringent polymers.



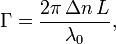

![E (\cos\theta\, \mathbf{\hat f} - \sin\theta\, \mathbf{\hat s})\mathrm{e}^{i(kz-\omega t)} = E [\cos(-\theta) \mathbf{\hat f} + \sin(-\theta) \mathbf{\hat s}]\mathrm{e}^{i(kz-\omega t)}.](https://upload.wikimedia.org/math/3/1/4/3145409fbe3b284da9098b1b956f793c.png)


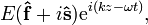

No comments:
Post a Comment