Optics
- Optical physics studies the interactions of light with atoms, molecules and semiconductor systems in different contexts. At the College of Optical Sciences, nine different research groups pursue projects in quantum gases, quantum information, theoretical and computational optical physics, experimental and theoretical semiconductor quantum optics, and ultrafast lasers, with impacts to the theory and applications of high-harmonic generation, laser cooling and trapping, quantum control, and much more.
- The Theoretical Solid-State Optics Group led by Rolf Binder focuses on the optical properties of semiconductor structures. Using microscopic quantum-mechanical many-body theories, including nonequilibrium Green's functions, the group pursues projects ranging from basic physical studies to application-oriented simulations. Recent and ongoing examples include slow- and fast-light effects in bulk semiconductors and semiconductor heterostructures, optical refrigeration of semiconductors, optical and elastic properties of semiconductor nanomembranes, optical properties of graphene, and pattern formation and control in quantum fluids realized by exciton polaritons in semiconductor microcavities.
-
QUANTUM NANO-OPTICS GROUP
- Galina Khitrova's Quantum Nano-Optics of Semiconductors Group conducts experimental studies of the light-matter interaction of semiconductor heterostructures (quantum wells and dots) coupled to nanoscale optical cavities. Recently, this has led to the investigation of metallic cavities that allow light to be confined to regions one thousand times smaller than typical dielectric cavities, which creates a large vacuum electromagnetic field that greatly alters the dynamics of the c oupled quantum emitter. Among the group's goals is to use these nanocavities to demonstrate Purcell enhancement of spontaneous emission and cooperative emission from semiconductor quantum dots.

THEORETICAL AND COMPUTATIONAL OPTICAL PHYSICS GROUP
- The Theoretical and Computational Optical Physics Group led by Miroslav Kolesik explores the intersection of modern nonlinear optics, atomic and molecular physics, and strong-field phenomena. Research interests span statistical mechanics, Monte Carlo simulation, critical phenomena, nonequilibrium and driven systems, semiconductor laser simulation and optics; current activity concentrates on computational optics, particularly ultrashort optical pulse interactions.Recent work includes first-principle methods to describe light-matter interactions in regimes that defy the tools and notions of traditional nonlinear optics and that scale from the quantum through the optical to the macroscopic. The challenge is in the integration of the microscopic medium description into space- and time-resolved, realistic simulations of experiments. Substantial research is being done in close collaboration with teams in the U.S. and Europe.
OPTICAL PHYSICS GROUP
- Masud Mansuripur's Optical Physics Group researches optical-magnetic-macromolecular data storage, light-matter interaction, magneto-optical effects and the mechanical effects of light involving the exchange of linear and angular momenta between electromagnetic fields and material media.As an example of the latter effects, the figure above shows a hollow metallic cone with an apex angle of 90 degrees, illuminated by a circularly polarized light beam. Upon reflection from the cone, the spin angular momentum of the beam is reversed. However, no angular momentum is transferred to the cone, because the reflected beam picks up an orbital angular momentum twice as large but opposite in direction to that of its spin. The figure also shows profiles of the phase and the Poynting vector in the cross-sectional plane of the reflected beam.
- 2. interference in thin film by reflection
- Thin-film interference occurs when incident light waves reflected by the upper and lower boundaries of a thin film interferewith one another to form a new wave. Studying this new wave can reveal information about the surfaces from which its components reflected, including the thickness of the film or the effective refractive index of the film medium. Thin films have many commercial applications including anti-reflection coatings, mirrors, and optical filters.
-
Consider light incident on a thin film and reflected by both the upper and lower boundaries. The optical path difference (OPD) of the reflected light must be calculated in order to determine the condition for interference. Referring to the ray diagram above, the OPD between the two waves is the following:
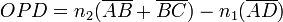
Where,


Using Snell's Law, 



Interference will be constructive if the optical path difference is equal to an integer multiple of the wavelength of light,  .
.

This condition may change after considering possible phase shifts that occur upon reflection
Consider light incident on a thin film and reflected by both the upper and lower boundaries. The optical path difference (OPD) of the reflected light must be calculated in order to determine the condition for interference. Referring to the ray diagram above, the OPD between the two waves is the following:
Where,
Using Snell's Law, 

Interference will be constructive if the optical path difference is equal to an integer multiple of the wavelength of light,  .
.
 .
.
This condition may change after considering possible phase shifts that occur upon reflection
Reflection Phase Change
Reflected light will experience a 180 degree phase change when it reflects from a medium of higher index of refraction and no phase change when it reflects from a medium of smaller index. This phase change is important in the interference which occurs in thin films, the design of anti-reflection coatings, interference filters, and thin film mirrors.-
Thin Films
The optical properties of thin films arise from interference and reflection. The basic conditions for interference depend upon whether the reflections involve 180 degree phase changes.



- Reflection and Interference from Thin Films PDF
- 35-4. Interference in Thin Films PDF
Thin Film Interference
- The emphasis of Lesson 1 of this unit is to present some evidence that has historically supported the view that light behaves as a wave. The reflection, refraction and diffraction of light waves is one strand of evidence. The interference of light waves is a second strand of evidence. In the early nineteenth century, Thomas Young showed that the interference of light passing through two slits produces an interference pattern when projected on a screen. In this section of Lesson 1, we will investigate another example of interference that provides further evidence in support of the wavelike behavior of light.Perhaps you have witnessed streaks of color on a car windshield shortly after it has been swiped by a windshield wiper or a squeegee at a gas station. The momentary streaks of color are the result of interference of light by the very thin film of water or soap that remains on the windshield. Or perhaps you have witnessed streaks of color in a thin film of oil resting upon a water puddle or concrete driveway. These streaks of color are the result of the interference of light by the very thin film of oil that is spread over the water surface. This form of interference is commonly called thin film interference and provides another line of evidence for the wave behavior of lightLight wave interference results when two waves are traveling through a medium and meet up at the same location. So what exactly is causing this thin film interference? What is the source of the two waves? When a wave (light waves included) reaches the boundary between two media, a portion of the wave reflects off the boundary and a portion is transmitted across the boundary. The reflected portion of the wave remains in the original medium. The transmitted portion of the wave enters the new medium and continues traveling through it until it reaches a subsequent boundary. If the new medium is a thin film, then the transmitted wave does not travel far before it reaches a new boundary and undergoes the usualreflection and transmission behavior. Thus, there are two waves that emerge from the film - one wave that is reflected off the top of the film (wave 1 in the diagram) and the other wave that reflects off the bottom of the film (wave 2 in the diagram).
These two waves could interfere constructively if they meet two conditions. One condition is that the two waves must be relatively close together such that their crests and troughs can meet up with each other and cause the interference. To meet this condition, the light must be incident at angles close to zero with respect to the normal. (This is not shown in the diagram above in order to space out the waves for clarity sake.) A second condition that must be met is that the wave that travels through the film and back into the original medium must have traveled just the right distance such that it is in phase with the other reflected wave. Two waves that are in phase are waves that are always at the same point on their wave cycle. That is, the two waves must be forming crests at the same location and at the same moment in time and forming troughs at the same location and at the same moment in time. In order for the second condition to occur, the thickness of the film must be just perfect.If wave 1 and wave 2 meet these two conditions as they reflect and exit the film, then they will constructively interfere. As will be learned in Lesson 2, light that is visible to our eyes consists of a collection of light waves of varying wavelength. Each wavelength is characterized by its own color. So a red light wave has a different wavelength than an orange light wave that has a different wavelength than a yellow light wave. While the thickness of a film at a given location may not allow a red and an orange light wave to emerge from the filmin phase, it may be just perfect to allow a yellow light wave to emerge in phase. So at a given location on the film, the yellow light wave undergoes constructive interference and becomes brighter than the other colors within the incident light. As such, the film appears yellow when viewed by incident sunlight. Other locations of the film may be just perfect to constructively reinforce red light. And still others area of the film may be of perfect thickness for the constructive reinforcement of green light. Because different locations of the film may be of appropriate thickness to reinforce different colors of light, the thin film will show streaks of color when viewed from above.While the mathematics of thin film interference can become quite complicated, it is clear from this discussion that thin film interference is another phenomenon that can only be explained using a wave model of light - .

Newton's rings is a phenomenon in which an interference pattern is created by the reflection of light between two surfaces—a spherical surface and an adjacent flat surface. It is named after Isaac Newton, who first studied them in 1717.
- When a plano-convex lens with its convex surface is placed on a plane glass sheet, an air film of gradually increasing thickness outward is formed between the lens and the sheet. The thickness of film at the point of contact is zero. If monochromatic light is allowed to fall normally on the lens, and the film is viewed in reflected light, alternate bright and dark concentric rings are seen around the point of contact. These rings were first discovered by Newton, that's why they are called NEWTON'S RINGS .
- Newton's rings are formed due to interference between the light waves reflected from the top and bottom surfaces of the air film formed between the lens and glass sheet.
The phenomenon of the formation of the Newton's rings can be explained on the basis of wave theory of light. An air film of varying thickness is formed between the lens and the glass sheet. 
The sketch at left shows the global geometry. The convex side of the lens has a radius of curvature R and we consider one of the rigns with radius r where the air film between lens and flat has thickness t. We analyse this geometry below.
At right we see a photograph of the interference pattern. The large dark patch at the centre is around the point where the convex lens surface touches the glass flat below it. In this area, the thin film of air between the lens and the flat has a thickness much less than the wavelength of light. This is surrounded by bright and dark circles, due to constructive and destructive interference respectively.
At right we see a photograph of the interference pattern. The large dark patch at the centre is around the point where the convex lens surface touches the glass flat below it. In this area, the thin film of air between the lens and the flat has a thickness much less than the wavelength of light. This is surrounded by bright and dark circles, due to constructive and destructive interference respectively.
Reflections and the conditions for constructive and destructive interferenceThis sketch shows the geometry close to the point* of contact between the convext lens (top) and glass flat (bottom). The other surfaces (the top surface of the lens and the bottom surface of the flat) are assumed to be so far away that reflections from them don't produce interference fringes: see Coherence length.
Now consider the phase difference due to reflections. (See Reflections and phases for an introduction.) At the upper surface, the ray reflects going from glass towards air – high n to low n – so the phase change is zero, as indicated on the sketch. At the lower surface, the ray reflects going from air towards glass – low n to high – so the phase change is π. So, with small phase change due to path length but a π phase change due to the two reflections, these two rays are about π radians or half of one cycle out of phase, which gives destructive interference. Consequence: in this region close to the point of contact, there is destructive interference in reflection.  Next consider the middle set of rays in the sketch. Here the thickness is t = λ/4, so the path difference is 2t = λ/2. This gives a phase difference of π. Add this to the π from the reflections and the phase difference is 2π – the two rays are out of phase by one complete cycle. So, provided the coherence length is sufficiently long, these rays give constructive interference in reflection. Finally, the rays in the sketch at left are for an air film thickness of t = λ/2, so the path difference is 2t = λ. This gives a phase difference of 2π. Add this to the π from the reflections and the phase difference is 3π – the two rays are out of phase by one and a half complete cycles. This time we have destructive interference in reflection. Newton's rings in transmissionLet's consider a dark ring with radius r at a point where the separation is t. The right angled triangle shown in red has a height R–t so Pythagoras' theorem gives us
R2 = R2 − 2Rt + t2 + r2 and so 2Rt = t2 + r2
Thin film interference:
A film is said to be thin when its thickness is about the order of one wavelength of visible light which is taken to be 550 nm. When light is incident on such a film, a small portion gets reflected from the upper surface and a major portion is transmitted into the film. Again a small part of the transmitted component is reflected back into the film by the lower surface and the rest of it emerges out of the film. These reflected beams reunite to produce interference. Also the transmitted beams too interfere. This type of interference that takes place in thin films is called interference by division of amplitude.
Θ1 angle of incidence at medium 1 to medium 2 boundary.
Θ2 angle of refraction at medium 1 to medium 2 boundary. Θ3 angle of refraction at medium 2 to medium 3 boundary. r12 reflected light from medium 1 to medium 2 boundary. r23 reflected light from medium 2 to medium 1 boundary. r21 reflected light from medium 2 to medium 3 boundary. t21 transmitted light from medium 2 to medium 1 boundary. t23 transmitted light from medium 2 to medium 3 boundary. d thickness of the film.
In the above figure the rays r12 and t21 interfere and results in a constructive or destructive interference depending on their path differences, given as,
Where,
The transmitted light from t23 can also interfere and result in constructive or destructive interference. Thin film interference with films of varying thickness (Newton’s rings):
Rings are fringes of equal thickness. They are observed when light is reflected from a plano-convex lens of a long focal length placed in contact with a plane glass plate. A thin air film is formed between the plate and the lens. The thickness of the air film varies from zero at the point of contact to some value t. If the lens plate system is illuminated with monochromatic light falling on it normally, concentric bright and dark interference rings are observed in reflected light. These circular fringes were discovered by Newton and are called Newton’s rings.
A ray AB incident normally on the system gets partially reflected at the bottom curved surface of the lens (Ray 1) and part of the transmitted ray is partially reflected (Ray 2) from the top surface of the plane glass plate. The rays 1 and 2 are derived from the same incident ray by division of amplitude and therefore are coherent. Ray 2 undergoes a phase change of p upon reflection since it is reflected from air-to-glass boundary.
The condition for constructive and destructive interferences are given as;
for normal incidence cos r = 1 and for air film
|










No comments:
Post a Comment