Theory of circularly polarized light

Theory of circularly polarized light

In electrodynamics, circular polarization of an electromagnetic wave is a polarization in which the electric field of the passing wave does not change strength but only changes direction in a rotary manner.

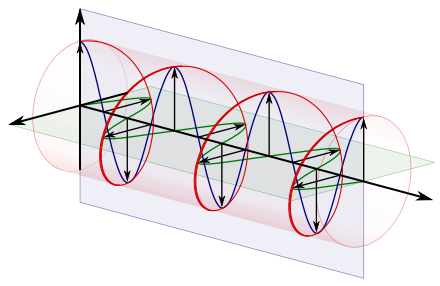
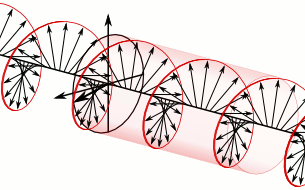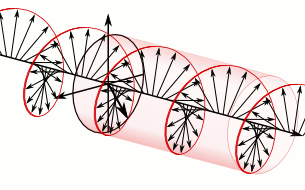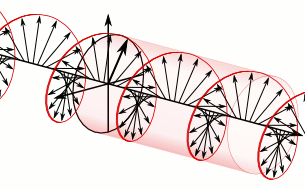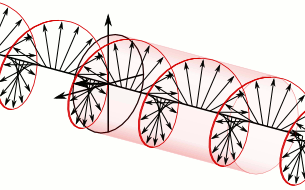
In electrodynamics the strength and direction of an electric field is defined by what is called an electric field vector. In the case of a circularly polarized wave, as seen in the accompanying animation, the tip of the electric field vector, at a given point in space, describes a circle as time progresses. If the wave is frozen in time, the electric field vector of the wave describes a helix along the direction of propagation.

Circular polarization is a limiting case of the more general condition of elliptical polarization. The other special case is the easier-to-understand linear polarization.

The phenomenon of polarization arises as a consequence of the fact that light behaves as a two-dimensional transverse wave.

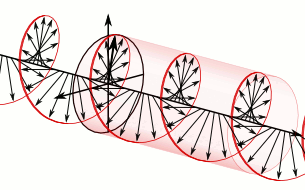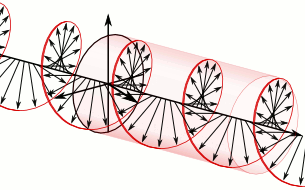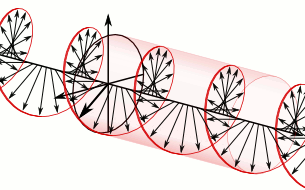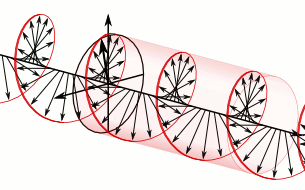
To appreciate how this quadrature phase shift corresponds to an electric field that rotates while maintaining a constant magnitude, imagine a dot traveling clockwise in a circle. Consider how the vertical and horizontal displacements of the dot, relative to the center of the circle, vary sinusoidally in time and are out of phase by one quarter of a cycle. The displacements are said to be out of phase by one quarter of a cycle because the horizontal maximum displacement (toward the left) is reached one quarter of a cycle before the vertical maximum displacement is reached. Now referring again to the illustration, imagine the center of the circle just described, traveling along the axis from the front to the back. The circling dot will trace out a helix with the displacement toward our viewing left, leading the vertical displacement. Just as the horizontal and vertical displacements of the rotating dot are out of phase by one quarter of a cycle in time, the magnitude of the horizontal and vertical components of the electric field are out of phase by one quarter of a wavelength.

Reversal of Handedness by Phase Shift

To convert a given handedness of polarized light to the other handedness one can use a half-wave plate. A half-wave plate shifts a given component of light one half of a wavelength relative to the component to which it is orthogonal.

Reversal of Handedness by Reflection

The handedness of polarized light is also reversed when it is reflected off of a surface at normal incidence. Upon such reflection, the rotation of the plane of polarization of the reflected light is identical to that of the incident field. However with propagation now in the opposite direction, the same rotation direction that would be described as "right handed" for the incident beam, is "left-handed" for propagation in the reverse direction, and vice versa. Aside from the reversal of handedness, the ellipticity of polarization is also preserved (except in cases of reflection by a birefringent surface).

From the point of view of the source

Using this convention, polarization is defined from the point of view of the source. When using this convention, left or right handedness is determined by pointing one's left or right thumb away from the source, in the same direction that the wave is propagating, and matching the curling of one's fingers to the direction of the temporal rotation of the field at a given point in space. When determining if the wave is clockwise or anti-clockwise circularly polarized, one again takes the point of view of the source, and while looking away from the source and in the same direction of the wave’s propagation, one observes the direction of the field’s temporal rotation.

Using this convention, the electric field vector of a right handed circularly polarized wave is as follows: 

Light and Polarization

This section will introduce some of the basic concepts that are important in understanding the optical behavior of liquid crystals. This is by no means a complete discussion of the topic; it is only intended to be used in the context of liquid crystal optical behavior. Please refer to Jenkins and White for a detailed treatment.

Light and Polarization

Light can be represented as a transverse electromagnetic wave made up of mutually perpendicular, fluctuating electric and magnetic fields. The left side of the following diagram shows the electric field in the xy plane, the magnetic field in the xz plane and the propagation of the wave in the x direction. The right half shows a line tracing out the electric field vector as it propagates. Traditionally, only the electric field vector is dealt with because the magnetic field component is essentially the same.

This sinusoidally varying electric field can be thought of as a length of rope held by two children at opposite ends. The children begin to displace the ends in such a way that the rope moves in a plane, either up and down, left and right, or at any angle in between.
Ordinary white light is made up of waves that fluctuate at all possible angles. Light is considered to be "linearly polarized" when it contains waves that only fluctuate in one specific plane. It is as if the rope is strung through a picket fence -- the wave can move up and down, but motion is blocked in any other direction. A polarizer is a material that allows only light with a specific angle of vibration to pass through. The direction of fluctuation passed by the polarizer is called the "easy" axis.
If two polarizers are set up in series so that their optical axes are parallel, light passes through both. However, if the axes are set up 90 degrees apart (crossed), the polarized light from the first is extinguished by the second. As the angle rotates from 0 to 90 degrees, the amount of light that is transmitted decreases. This effect is demonstrated in the following diagram. The polarizers are parallel at the top and crossed at the bottom.

Polarized Light

Linear polarization is merely a special case of circularly polarized light. Consider two light waves, one polarized in the YZ plane and the other in the XY plane. If the waves reach their maximum and minimum points at the same time (they are in phase), their vector sum leads to one wave, linearly polarized at 45 degrees. This is shown in the following diagram.

Similarly, if the two waves are 180 degrees out of phase, the resultant is linearly polarized at 45 degrees in the opposite sense.

If the two waves are 90 degrees out of phase (one is at an extremum and the other is at zero), the resulting wave is circularly polarized. In effect, the resultant electric field vector from the sum of the components rotates around the origin as the wave propagates. The following diagram shows the sum of the electric field vectors for two such waves.

The most general case is when the phase difference is at an arbitrary angle (not necessarily 90 or 180 degrees.) This is called elliptical polarization because the electric field vector traces out an ellipse (instead of a line or circle as before.)

Classification of Polarization

Light in the form of a plane wave in space is said to be linearly polarized. Light is a transverse electromagnetic wave, but natural light is generally un-polarized, all planes of propagation being equally probable. If light is composed of two plane waves of equal amplitude by differing in phase by 90°, then the light is said to be circularly polarized. If two plane waves of differing amplitude are related in phase by 90°, or if the relative phase is other than 90° then the light is said to be elliptically polarized.



pdf1
pdf2
pdf3